स्टूडेंट्स आप चैप्टर 8 के तहत त्रिभुजों से संबंधित त्रिकोणमिति का अध्ययन करेंगे। इस अध्याय में आपको त्रिभुज के अनुपात , त्रिकोणमितिय विशिष्ट अनुपात, त्रिकोणमितीय सर्वसमिका आदि के बारे में बताया गया है। हमारे इस आर्टिकल में आप चैप्टर 8 NCERT Solution for Class 10 Maths Chapter 8 (Introduction of Trigonometry) के प्रश्न के solutions प्राप्त कर सकते हैं एवं संबंधित पीडीऍफ़ भी डाउनलोड कर सकते हैं।
Summary (सारांश) of Introduction of Trigonometry
- यदि समकोण त्रिभुज ABC में , जिसका कोण B समकोण है। तब त्रिकोणमितीय अनुपात होंगे जो इस प्रकार से हैं
sin A = कोण A की सम्मुख भुजा / कर्ण
cos A = कोण A की संलंग्न भुजा / कर्ण
tan A = कोण A की सम्मुख भुजा / कोण A की संलग्न भुजा
cosec A = 1 / sin A
sec A = 1 / cos A
tan A = 1 / cot A
tan A = sin A / cos A
- त्रिकोणमिति में गणनाओं के लिए विशिष्ट अनुपातों का उपयोग किया जाता है। हमने यहाँ सारणी (Table) के माध्यम से आपको इन विशिष्ट अनुपातों के बारे में बताया है। टेबल में आप देख सकते हैं की आप जैसे – जैसे Sine के कोण A का मान 0० से 90० के बीच रखते हैं तो sine A का मान कोण की डिग्री के अनुसार बदलता रहता है। आप टेबल में देख सकते हैं।
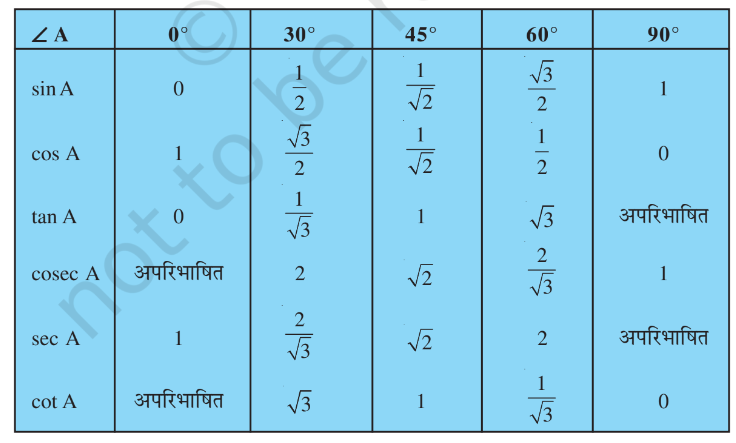
- sin A या cos A का मान कभी भी 1 से अधिक नहीं होता , जबकि sec A या cosec A का मान सदैव 1 से अधिक या 1 के बराबर होता है।
- यदि किसी समकोण त्रिभुज में दो कोंण पूरक कोण हो तो उनका योग 90० होता है। पूरक कोण से संबंधित त्रिकोणमितीय अनुपातों के लिए सूत्र इस प्रकार से है।
sin (90० – A) = cos A
cos (90० – A) = sin A
tan (90० – A) = cot A
cot (90० – A) = tan A
sec (90० – A) = cosec A
cosec (90० – A) = sec A
- त्रिकोणमिति सर्वसमिकाएँ से संबंधित सूत्र (formulas)
cos2A + sin2A = 1
1 + tan2A = sec2A जहाँ 0° ≤ A < 90°
cot2A + 1 = cosec2A जहाँ 0° < A ≤ 90o
- यदि किसी त्रिभुज में एक न्यून कोण का त्रिकोणमितीय अनुपात ज्ञात हो तो शेष कोणों के त्रिकोणमितीय अनुपात आसानी से ज्ञात किये जा सकते हैं।
Trigonometry से संबंधित उदाहरण
यदि आप त्रिकोणमिति से संबंधित अन्य उदाहरण देखना चाहते हैं आप आर्टिकल में दी गयी पीडीऍफ़ फाइल में देख सकते हैं।
प्रश्नावली 8.1 ( त्रिकोणमिति अनुपात ) के सॉलूशन्स
प्रश्नावली 8.2 ( कुछ विशिष्ट कोणों के त्रिकोणमिति अनुपात ) के सॉलूशन्स
प्रश्नावली 8.3 ( पूरक कोणों के त्रिकोणमिति अनुपात ) के सॉलूशन्स
प्रश्नावली 8.4 ( त्रिकोणमिति सर्वसमिकएं ) के सॉलूशन्स
स्टूडेंट्स यदि आप प्रश्नावलियों से संबंधित अन्य प्रश्न के Solutions देखना चाहते हैं तो आप नीचे दी गयी पीडीऍफ़ फाइल में Solutions देख सकते हैं।
Frequently Asked Question (FAQs)
स्टूडेंट हम आपको बता दें की त्रिकोणमिति का अर्थ होता है “त्रिभुज का मापन” त्रिकोणमिति (Trigonometry) गणित की एक ऐसी शाखा है जिसमें त्रिभुजों से बनने वाली आकृति और कोणों के अनुपात का अध्ययन किया जाता है।
त्रिकोणमिति में कुल 6 अनुपात हैं (Sin , Cos , Tan , Cot , Sec एवं CoSec)
जिस त्रिभुज में एक कोण 90o हो वह त्रिभुज समकोण त्रिभुज कहलाता है।
त्रिभुज के सभी कोणों का योग दो समकोण अर्थात (90o + 90० ) या 180o के बराबर होता है।
